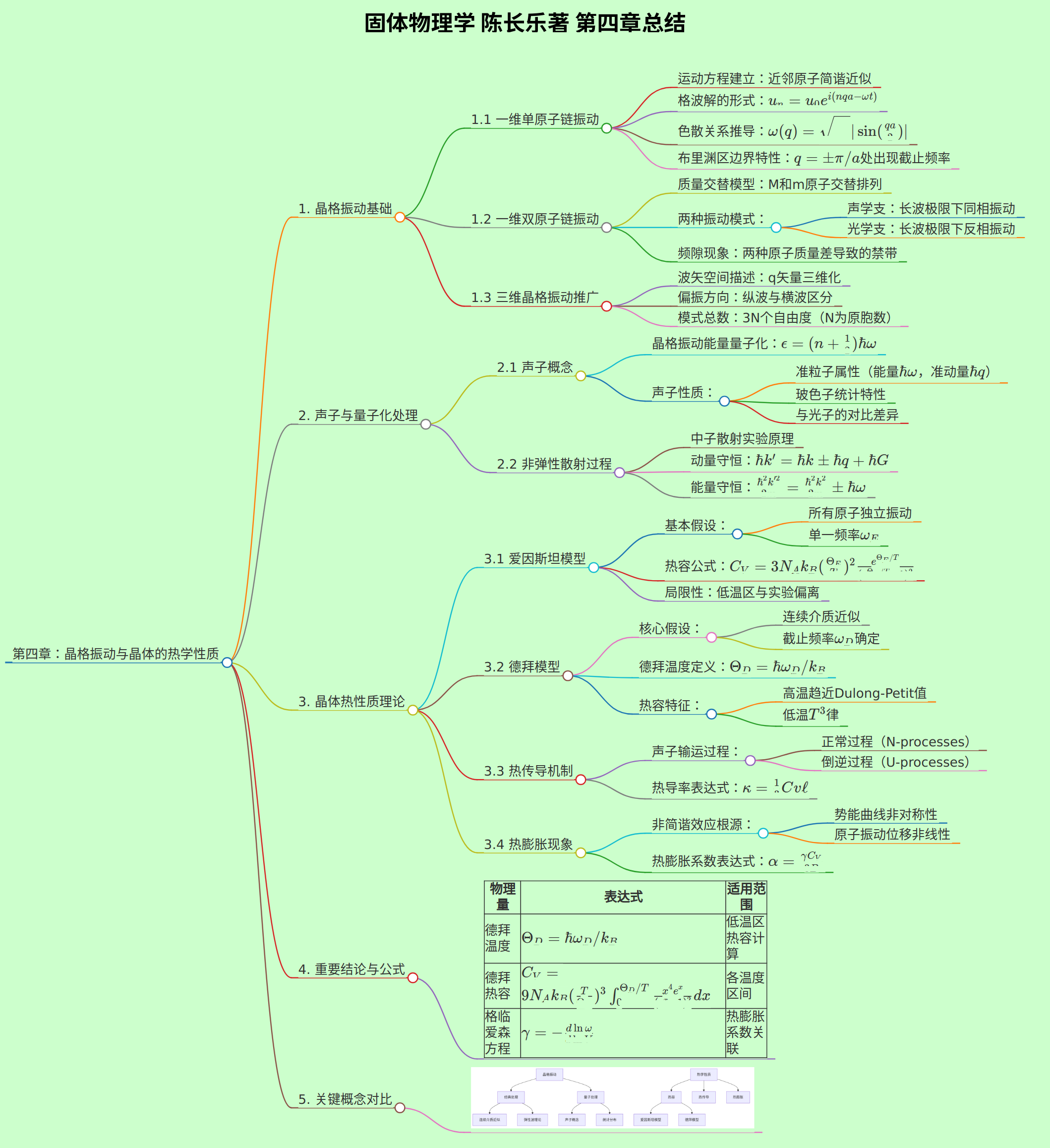
- ```markdown # 固体物理学 陈长乐著 第四章总结 ## 第四章：晶格振动与晶体的热学性质 ### 1. 晶格振动基础 #### 1.1 一维单原子链振动 - 运动方程建立：近邻原子简谐近似 - 格波解的形式：$u_n = u_0 e^{i(nqa - \omega t)}$ - 色散关系推导：$\omega(q) = \sqrt{\frac{4\beta}{m}}|\sin(\frac{qa}{2})|$ - 布里渊区边界特性：$q=\pm\pi/a$处出现截止频率 #### 1.2 一维双原子链振动 - 质量交替模型：M和m原子交替排列 - 两种振动模式： - 声学支：长波极限下同相振动 - 光学支：长波极限下反相振动 - 频隙现象：两种原子质量差导致的禁带 #### 1.3 三维晶格振动推广 - 波矢空间描述：q矢量三维化 - 偏振方向：纵波与横波区分 - 模式总数：3N个自由度（N为原胞数） ### 2. 声子与量子化处理 #### 2.1 声子概念 - 晶格振动能量量子化：$\epsilon = (n+\frac{1}{2})\hbar\omega$ - 声子性质： - 准粒子属性（能量$\hbar\omega$，准动量$\hbar q$） - 玻色子统计特性 - 与光子的对比差异 #### 2.2 非弹性散射过程 - 中子散射实验原理 - 动量守恒：$\hbar k' = \hbar k \pm \hbar q + \hbar G$ - 能量守恒：$\frac{\hbar^2k'^2}{2m} = \frac{\hbar^2k^2}{2m} \pm \hbar\omega$ ### 3. 晶体热性质理论 #### 3.1 爱因斯坦模型 - 基本假设： - 所有原子独立振动 - 单一频率$\omega_E$ - 热容公式：$C_V = 3N_Ak_B(\frac{\Theta_E}{T})^2\frac{e^{\Theta_E/T}}{(e^{\Theta_E/T}-1)^2}$ - 局限性：低温区与实验偏离 #### 3.2 德拜模型 - 核心假设： - 连续介质近似 - 截止频率$\omega_D$确定 - 德拜温度定义：$\Theta_D = \hbar\omega_D/k_B$ - 热容特征： - 高温趋近Dulong-Petit值 - 低温$T^3$律 #### 3.3 热传导机制 - 声子输运过程： - 正常过程（N-processes） - 倒逆过程（U-processes） - 热导率表达式：$\kappa = \frac{1}{3}Cv\ell$ #### 3.4 热膨胀现象 - 非简谐效应根源： - 势能曲线非对称性 - 原子振动位移非线性 - 热膨胀系数表达式：$\alpha = \frac{\gamma C_V}{3B}$ ### 4. 重要结论与公式 | 物理量 | 表达式 | 适用范围 | |--------|--------|----------| | 德拜温度 | $\Theta_D = \hbar\omega_D/k_B$ | 低温区热容计算 | | 德拜热容 | $C_V = 9N_Ak_B(\frac{T}{\Theta_D})^3\int_0^{\Theta_D/T}\frac{x^4e^x}{(e^x-1)^2}dx$ | 各温度区间 | | 格临爱森方程 | $\gamma = -\frac{d\ln\omega}{d\ln V}$ | 热膨胀系数关联 | ### 5. 关键概念对比