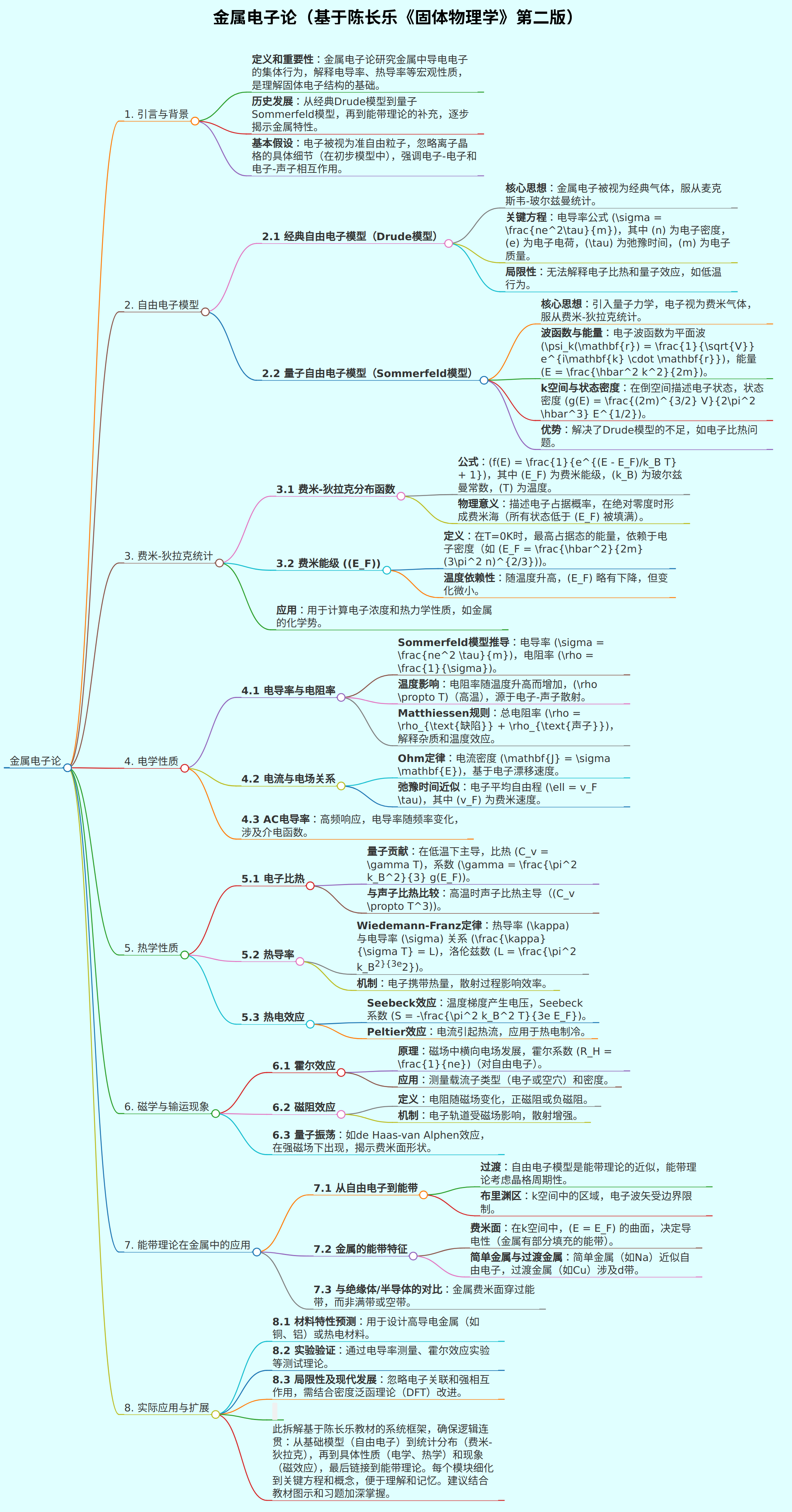
### 金属电子论（基于陈长乐《固体物理学》第二版） - 金属电子论是固体物理学中的核心内容，专注于金属中电子的行为、性质和理论模型。陈长乐第二版教材中，该部分系统阐述了从经典到量子模型的演变，强调自由电子模型、统计分布和物理性质的计算。以下是完整拆解，确保准确性和易记性。拆解基于教材结构，分为主要模块（一级标题），再细分子模块（二级标题）和关键点（列表形式），覆盖核心概念、模型、性质和应用。 - ```markdown # 金属电子论 ## 1. 引言与背景 - **定义和重要性**：金属电子论研究金属中导电电子的集体行为，解释电导率、热导率等宏观性质，是理解固体电子结构的基础。 - **历史发展**：从经典Drude模型到量子Sommerfeld模型，再到能带理论的补充，逐步揭示金属特性。 - **基本假设**：电子被视为准自由粒子，忽略离子晶格的具体细节（在初步模型中），强调电子-电子和电子-声子相互作用。 ## 2. 自由电子模型 - **2.1 经典自由电子模型（Drude模型）** - **核心思想**：金属电子被视为经典气体，服从麦克斯韦-玻尔兹曼统计。 - **关键方程**：电导率公式 \(\sigma = \frac{ne^2\tau}{m}\)，其中 \(n\) 为电子密度，\(e\) 为电子电荷，\(\tau\) 为弛豫时间，\(m\) 为电子质量。 - **局限性**：无法解释电子比热和量子效应，如低温行为。 - **2.2 量子自由电子模型（Sommerfeld模型）** - **核心思想**：引入量子力学，电子视为费米气体，服从费米-狄拉克统计。 - **波函数与能量**：电子波函数为平面波 \(\psi_k(\mathbf{r}) = \frac{1}{\sqrt{V}} e^{i\mathbf{k} \cdot \mathbf{r}}\)，能量 \(E = \frac{\hbar^2 k^2}{2m}\)。 - **k空间与状态密度**：在倒空间描述电子状态，状态密度 \(g(E) = \frac{(2m)^{3/2} V}{2\pi^2 \hbar^3} E^{1/2}\)。 - **优势**：解决了Drude模型的不足，如电子比热问题。 ## 3. 费米-狄拉克统计 - **3.1 费米-狄拉克分布函数** - **公式**：\(f(E) = \frac{1}{e^{(E - E_F)/k_B T} + 1}\)，其中 \(E_F\) 为费米能级，\(k_B\) 为玻尔兹曼常数，\(T\) 为温度。 - **物理意义**：描述电子占据概率，在绝对零度时形成费米海（所有状态低于 \(E_F\) 被填满）。 - **3.2 费米能级 (\(E_F\))** - **定义**：在T=0K时，最高占据态的能量，依赖于电子密度（如 \(E_F = \frac{\hbar^2}{2m} (3\pi^2 n)^{2/3}\))。 - **温度依赖性**：随温度升高，\(E_F\) 略有下降，但变化微小。 - **应用**：用于计算电子浓度和热力学性质，如金属的化学势。 ## 4. 电学性质 - **4.1 电导率与电阻率** - **Sommerfeld模型推导**：电导率 \(\sigma = \frac{ne^2 \tau}{m}\)，电阻率 \(\rho = \frac{1}{\sigma}\)。 - **温度影响**：电阻率随温度升高而增加，\(\rho \propto T\)（高温），源于电子-声子散射。 - **Matthiessen规则**：总电阻率 \(\rho = \rho_{\text{缺陷}} + \rho_{\text{声子}}\)，解释杂质和温度效应。 - **4.2 电流与电场关系** - **Ohm定律**：电流密度 \(\mathbf{J} = \sigma \mathbf{E}\)，基于电子漂移速度。 - **弛豫时间近似**：电子平均自由程 \(\ell = v_F \tau\)，其中 \(v_F\) 为费米速度。 - **4.3 AC电导率**：高频响应，电导率随频率变化，涉及介电函数。 ## 5. 热学性质 - **5.1 电子比热** - **量子贡献**：在低温下主导，比热 \(C_v = \gamma T\)，系数 \(\gamma = \frac{\pi^2 k_B^2}{3} g(E_F)\)。 - **与声子比热比较**：高温时声子比热主导（\(C_v \propto T^3\))。 - **5.2 热导率** - **Wiedemann-Franz定律**：热导率 \(\kappa\) 与电导率 \(\sigma\) 关系 \(\frac{\kappa}{\sigma T} = L\)，洛伦兹数 \(L = \frac{\pi^2 k_B^2}{3e^2}\)。 - **机制**：电子携带热量，散射过程影响效率。 - **5.3 热电效应** - **Seebeck效应**：温度梯度产生电压，Seebeck系数 \(S = -\frac{\pi^2 k_B^2 T}{3e E_F}\)。 - **Peltier效应**：电流引起热流，应用于热电制冷。 ## 6. 磁学与输运现象 - **6.1 霍尔效应** - **原理**：磁场中横向电场发展，霍尔系数 \(R_H = \frac{1}{ne}\)（对自由电子）。 - **应用**：测量载流子类型（电子或空穴）和密度。 - **6.2 磁阻效应** - **定义**：电阻随磁场变化，正磁阻或负磁阻。 - **机制**：电子轨道受磁场影响，散射增强。 - **6.3 量子振荡**：如de Haas-van Alphen效应，在强磁场下出现，揭示费米面形状。 ## 7. 能带理论在金属中的应用 - **7.1 从自由电子到能带** - **过渡**：自由电子模型是能带理论的近似，能带理论考虑晶格周期性。 - **布里渊区**：k空间中的区域，电子波矢受边界限制。 - **7.2 金属的能带特征** - **费米面**：在k空间中，\(E = E_F\) 的曲面，决定导电性（金属有部分填充的能带）。 - **简单金属与过渡金属**：简单金属（如Na）近似自由电子，过渡金属（如Cu）涉及d带。 - **7.3 与绝缘体/半导体的对比**：金属费米面穿过能带，而非满带或空带。 ## 8. 实际应用与扩展 - **8.1 材料特性预测**：用于设计高导电金属（如铜、铝）或热电材料。 - **8.2 实验验证**：通过电导率测量、霍尔效应实验等测试理论。 - **8.3 局限性及现代发展**：忽略电子关联和强相互作用，需结合密度泛函理论（DFT）改进。 - ``` - 此拆解基于陈长乐教材的系统框架，确保逻辑连贯：从基础模型（自由电子）到统计分布（费米-狄拉克），再到具体性质（电学、热学）和现象（磁效应），最后链接到能带理论。每个模块细化到关键方程和概念，便于理解和记忆。建议结合教材图示和习题加深掌握。