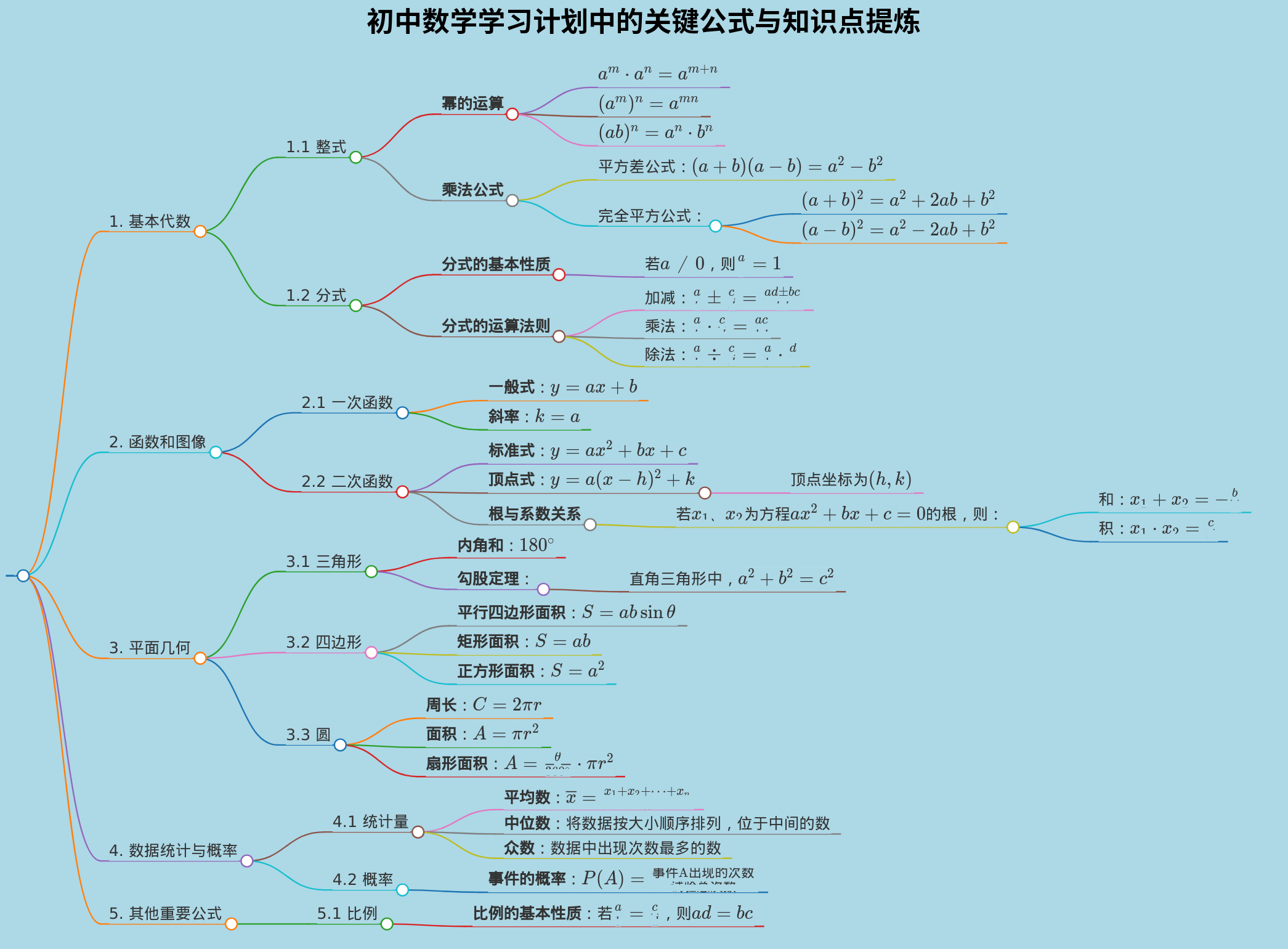
- 制定初中数学的学习计划时，了解并掌握重要的公式和概念是关键。以下是初中数学中常用的公式和知识点的详细拆解，以帮助学生更好地理解和记忆。 ## 1. 基本代数 ### 1.1 整式 - **幂的运算** - $a^m \cdot a^n = a^{m+n}$ - $(a^m)^n = a^{mn}$ - $(ab)^n = a^n \cdot b^n$ - **乘法公式** - 平方差公式：$(a+b)(a-b) = a^2 - b^2$ - 完全平方公式： - $(a+b)^2 = a^2 + 2ab + b^2$ - $(a-b)^2 = a^2 - 2ab + b^2$ ### 1.2 分式 - **分式的基本性质** - 若$a \neq 0$，则$\frac{a}{a} = 1$ - **分式的运算法则** - 加减：$\frac{a}{b} \pm \frac{c}{d} = \frac{ad \pm bc}{bd}$ - 乘法：$\frac{a}{b} \cdot \frac{c}{d} = \frac{ac}{bd}$ - 除法：$\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c}$ ## 2. 函数和图像 ### 2.1 一次函数 - **一般式**：$y = ax + b$ - **斜率**：$k = a$ ### 2.2 二次函数 - **标准式**：$y = ax^2 + bx + c$ - **顶点式**：$y = a(x-h)^2 + k$ - 顶点坐标为$(h, k)$ - **根与系数关系** - 若$x_1$、$x_2$为方程$ax^2+bx+c=0$的根，则： - 和：$x_1 + x_2 = -\frac{b}{a}$ - 积：$x_1 \cdot x_2 = \frac{c}{a}$ ## 3. 平面几何 ### 3.1 三角形 - **内角和**：$180^\circ$ - **勾股定理**： - 直角三角形中，$a^2 + b^2 = c^2$ ### 3.2 四边形 - **平行四边形面积**：$S = ab \sin\theta$ - **矩形面积**：$S = ab$ - **正方形面积**：$S = a^2$ ### 3.3 圆 - **周长**：$C = 2\pi r$ - **面积**：$A = \pi r^2$ - **扇形面积**：$A = \frac{\theta}{360^\circ} \cdot \pi r^2$ ## 4. 数据统计与概率 ### 4.1 统计量 - **平均数**：$\overline{x} = \frac{x_1 + x_2 + \cdots + x_n}{n}$ - **中位数**：将数据按大小顺序排列，位于中间的数 - **众数**：数据中出现次数最多的数 ### 4.2 概率 - **事件的概率**：$P(A) = \frac{\text{事件A出现的次数}}{\text{试验总次数}}$ ## 5. 其他重要公式 ### 5.1 比例 - **比例的基本性质**：若$\frac{a}{b} = \frac{c}{d}$，则$ad = bc$ 通过逐步掌握这些公式和知识点，学生能够更加自信地应对初中数学的学习和考试。每个模块都可以根据需要进一步分解，以便进行详细研究和练习。