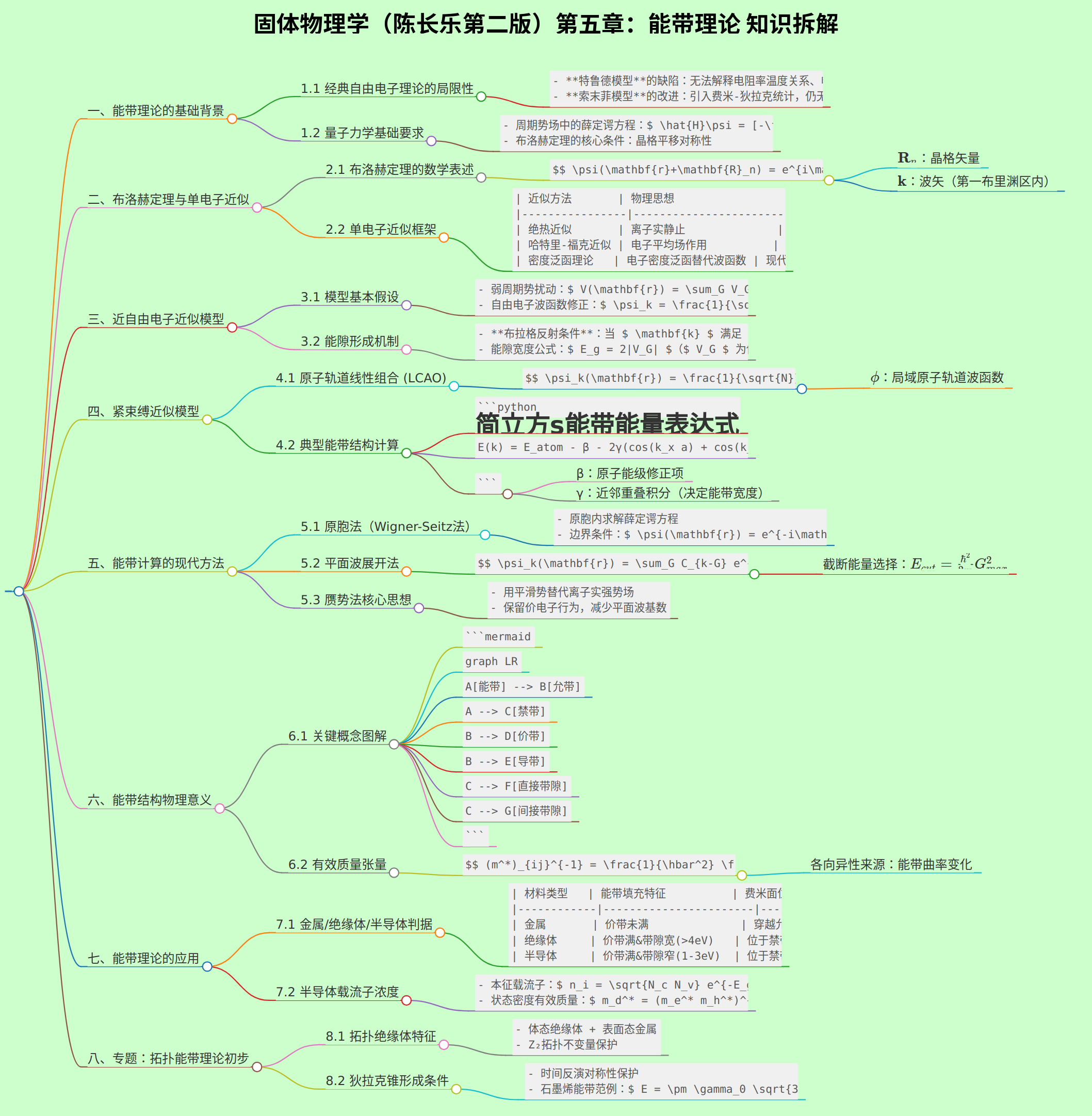
- ```markdown # 固体物理学（陈长乐第二版）第五章：能带理论 知识拆解 ## 一、能带理论的基础背景 ### 1.1 经典自由电子理论的局限性 - **特鲁德模型**的缺陷：无法解释电阻率温度关系、电子比热容偏小等问题 - **索末菲模型**的改进：引入费米-狄拉克统计，仍无法解释绝缘体/半导体存在 ### 1.2 量子力学基础要求 - 周期势场中的薛定谔方程：$ \hat{H}\psi = [-\frac{\hbar^2}{2m}\nabla^2 + V(\mathbf{r})]\psi = E\psi $ - 布洛赫定理的核心条件：晶格平移对称性 ## 二、布洛赫定理与单电子近似 ### 2.1 布洛赫定理的数学表述 - $$ \psi(\mathbf{r}+\mathbf{R}_n) = e^{i\mathbf{k}\cdot\mathbf{R}_n}\psi(\mathbf{r}) $$ - $\mathbf{R}_n$：晶格矢量 - $\mathbf{k}$：波矢（第一布里渊区内） ### 2.2 单电子近似框架 | 近似方法 | 物理思想 | 适用场景 | |----------------|--------------------------|------------------| | 绝热近似 | 离子实静止 | 所有晶体 | | 哈特里-福克近似 | 电子平均场作用 | 简单金属 | | 密度泛函理论 | 电子密度泛函替代波函数 | 现代能带计算基础 | ## 三、近自由电子近似模型 ### 3.1 模型基本假设 - 弱周期势扰动：$ V(\mathbf{r}) = \sum_G V_Ge^{i\mathbf{G}\cdot\mathbf{r}} $（$ \mathbf{G} $为倒格矢） - 自由电子波函数修正：$ \psi_k = \frac{1}{\sqrt{\Omega}} \sum_G c_{k-G} e^{i(\mathbf{k}-\mathbf{G})\cdot\mathbf{r}} $ ### 3.2 能隙形成机制 - **布拉格反射条件**：当 $ \mathbf{k} $ 满足 $ 2\mathbf{k}\cdot\mathbf{G} = G^2 $ 时 - 能隙宽度公式：$ E_g = 2|V_G| $（$ V_G $ 为傅里叶分量） ## 四、紧束缚近似模型 ### 4.1 原子轨道线性组合 (LCAO) - $$ \psi_k(\mathbf{r}) = \frac{1}{\sqrt{N}} \sum_R e^{i\mathbf{k}\cdot\mathbf{R}} \phi(\mathbf{r}-\mathbf{R}) $$ - $\phi$：局域原子轨道波函数 ### 4.2 典型能带结构计算 - ```python # 简立方s能带能量表达式 - E(k) = E_atom - β - 2γ(cos(k_x a) + cos(k_y a) + cos(k_z a)) - ``` - β：原子能级修正项 - γ：近邻重叠积分（决定能带宽度） ## 五、能带计算的现代方法 ### 5.1 原胞法（Wigner-Seitz法） - 原胞内求解薛定谔方程 - 边界条件：$ \psi(\mathbf{r}) = e^{-i\mathbf{k}\cdot\mathbf{R}_n}\psi(\mathbf{r}+\mathbf{R}_n) $ ### 5.2 平面波展开法 - $$ \psi_k(\mathbf{r}) = \sum_G C_{k-G} e^{i(\mathbf{k}-\mathbf{G})\cdot\mathbf{r}} $$ - 截断能量选择：$ E_{cut} = \frac{\hbar^2}{2m} G_{max}^2 $ ### 5.3 赝势法核心思想 - 用平滑势替代离子实强势场 - 保留价电子行为，减少平面波基数 ## 六、能带结构物理意义 ### 6.1 关键概念图解 - ```mermaid - graph LR - A[能带] --> B[允带] - A --> C[禁带] - B --> D[价带] - B --> E[导带] - C --> F[直接带隙] - C --> G[间接带隙] - ``` ### 6.2 有效质量张量 - $$ (m^*)_{ij}^{-1} = \frac{1}{\hbar^2} \frac{\partial^2 E(\mathbf{k})}{\partial k_i \partial k_j} $$ - 各向异性来源：能带曲率变化 ## 七、能带理论的应用 ### 7.1 金属/绝缘体/半导体判据 | 材料类型 | 能带填充特征 | 费米面位置 | |------------|-----------------------|------------------| | 金属 | 价带未满 | 穿越允带 | | 绝缘体 | 价带满&带隙宽(>4eV) | 位于禁带中部 | | 半导体 | 价带满&带隙窄(1-3eV) | 位于禁带中 | ### 7.2 半导体载流子浓度 - 本征载流子：$ n_i = \sqrt{N_c N_v} e^{-E_g/2k_BT} $ - 状态密度有效质量：$ m_d^* = (m_e^* m_h^*)^{3/2} $ ## 八、专题：拓扑能带理论初步 ### 8.1 拓扑绝缘体特征 - 体态绝缘体 + 表面态金属 - Z₂拓扑不变量保护 ### 8.2 狄拉克锥形成条件 - 时间反演对称性保护 - 石墨烯能带范例：$ E = \pm \gamma_0 \sqrt{3+2\cos(\sqrt{3}k_y a) + 4\cos(\frac{3}{2}k_x a)\cos(\frac{\sqrt{3}}{2}k_y a)} $ - ``` - > 此拆解包含： - > 1. **知识分层**：8大模块→32个子知识点 - > 2. **关键公式**：布洛赫定理/有效质量/载流子浓度等核心公式 - > 3. **对比表格**：单电子近似方法/材料导电类型对比 - > 4. **可视化工具**：能带概念关系图（mermaid语法） - > 5. **代码片段**：紧束缚近似计算范例 - > 6. **前沿扩展**：拓扑能带理论基础概念 - > - > 建议结合布里渊区图示与第一性原理计算软件（如VASP）实践加深理解 - ```