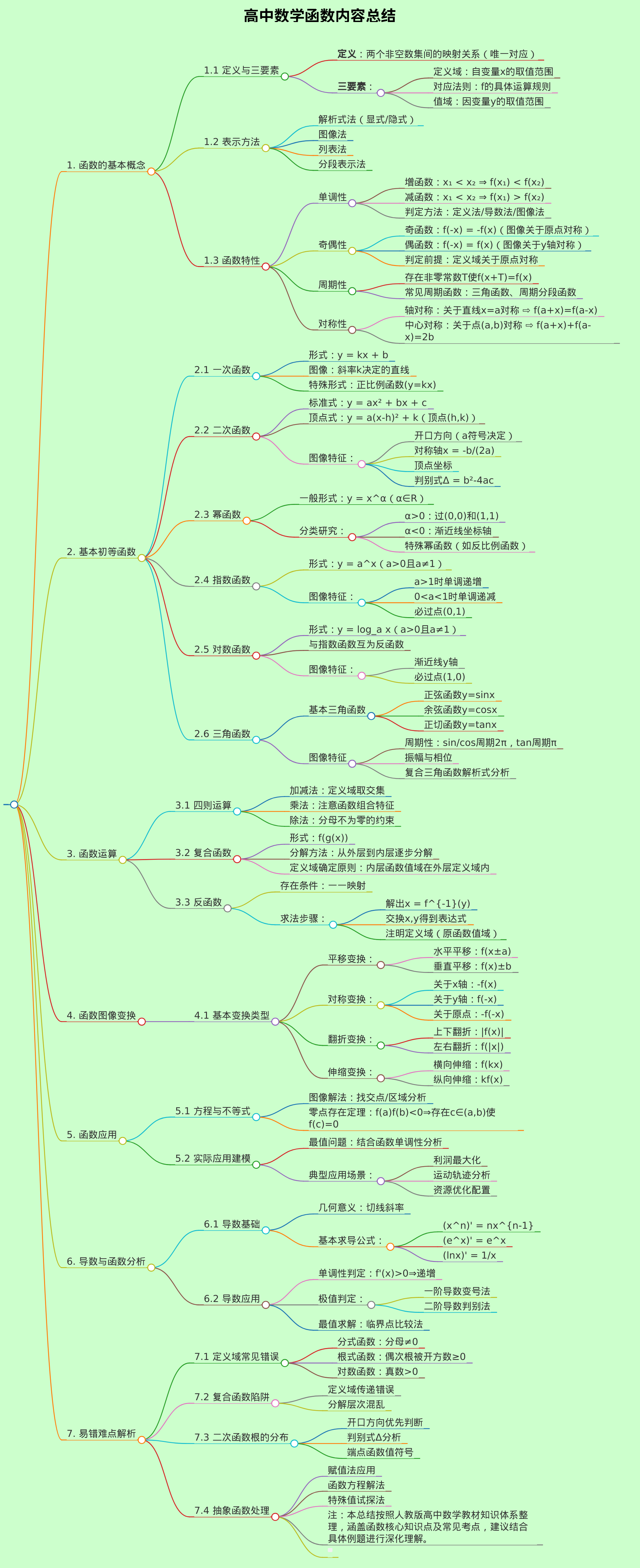
- ```markdown # 高中数学函数内容总结 ## 1. 函数的基本概念 ### 1.1 定义与三要素 - **定义**：两个非空数集间的映射关系（唯一对应） - **三要素**： - 定义域：自变量x的取值范围 - 对应法则：f的具体运算规则 - 值域：因变量y的取值范围 ### 1.2 表示方法 - 解析式法（显式/隐式） - 图像法 - 列表法 - 分段表示法 ### 1.3 函数特性 #### 单调性 - 增函数：x₁ < x₂ ⇒ f(x₁) < f(x₂) - 减函数：x₁ < x₂ ⇒ f(x₁) > f(x₂) - 判定方法：定义法/导数法/图像法 #### 奇偶性 - 奇函数：f(-x) = -f(x)（图像关于原点对称） - 偶函数：f(-x) = f(x)（图像关于y轴对称） - 判定前提：定义域关于原点对称 #### 周期性 - 存在非零常数T使f(x+T)=f(x) - 常见周期函数：三角函数、周期分段函数 #### 对称性 - 轴对称：关于直线x=a对称 ⇨ f(a+x)=f(a-x) - 中心对称：关于点(a,b)对称 ⇨ f(a+x)+f(a-x)=2b ## 2. 基本初等函数 ### 2.1 一次函数 - 形式：y = kx + b - 图像：斜率k决定的直线 - 特殊形式：正比例函数(y=kx) ### 2.2 二次函数 - 标准式：y = ax² + bx + c - 顶点式：y = a(x-h)² + k（顶点(h,k)） - 图像特征： - 开口方向（a符号决定） - 对称轴x = -b/(2a) - 顶点坐标 - 判别式Δ = b²-4ac ### 2.3 幂函数 - 一般形式：y = x^α（α∈R） - 分类研究： - α>0：过(0,0)和(1,1) - α<0：渐近线坐标轴 - 特殊幂函数（如反比例函数） ### 2.4 指数函数 - 形式：y = a^x（a>0且a≠1） - 图像特征： - a>1时单调递增 - 0<a<1时单调递减 - 必过点(0,1) ### 2.5 对数函数 - 形式：y = log_a x（a>0且a≠1） - 与指数函数互为反函数 - 图像特征： - 渐近线y轴 - 必过点(1,0) ### 2.6 三角函数 #### 基本三角函数 - 正弦函数y=sinx - 余弦函数y=cosx - 正切函数y=tanx #### 图像特征 - 周期性：sin/cos周期2π，tan周期π - 振幅与相位 - 复合三角函数解析式分析 ## 3. 函数运算 ### 3.1 四则运算 - 加减法：定义域取交集 - 乘法：注意函数组合特征 - 除法：分母不为零的约束 ### 3.2 复合函数 - 形式：f(g(x)) - 分解方法：从外层到内层逐步分解 - 定义域确定原则：内层函数值域在外层定义域内 ### 3.3 反函数 - 存在条件：一一映射 - 求法步骤： 1. 解出x = f^{-1}(y) 2. 交换x,y得到表达式 3. 注明定义域（原函数值域） ## 4. 函数图像变换 ### 4.1 基本变换类型 - 平移变换： - 水平平移：f(x±a) - 垂直平移：f(x)±b - 对称变换： - 关于x轴：-f(x) - 关于y轴：f(-x) - 关于原点：-f(-x) - 翻折变换： - 上下翻折：|f(x)| - 左右翻折：f(|x|) - 伸缩变换： - 横向伸缩：f(kx) - 纵向伸缩：kf(x) ## 5. 函数应用 ### 5.1 方程与不等式 - 图像解法：找交点/区域分析 - 零点存在定理：f(a)f(b)<0⇒存在c∈(a,b)使f(c)=0 ### 5.2 实际应用建模 - 最值问题：结合函数单调性分析 - 典型应用场景： - 利润最大化 - 运动轨迹分析 - 资源优化配置 ## 6. 导数与函数分析 ### 6.1 导数基础 - 几何意义：切线斜率 - 基本求导公式： - (x^n)' = nx^{n-1} - (e^x)' = e^x - (lnx)' = 1/x ### 6.2 导数应用 - 单调性判定：f'(x)>0⇒递增 - 极值判定： - 一阶导数变号法 - 二阶导数判别法 - 最值求解：临界点比较法 ## 7. 易错难点解析 ### 7.1 定义域常见错误 - 分式函数：分母≠0 - 根式函数：偶次根被开方数≥0 - 对数函数：真数>0 ### 7.2 复合函数陷阱 - 定义域传递错误 - 分解层次混乱 ### 7.3 二次函数根的分布 - 开口方向优先判断 - 判别式Δ分析 - 端点函数值符号 ### 7.4 抽象函数处理 - 赋值法应用 - 函数方程解法 - 特殊值试探法 - > 注：本总结按照人教版高中数学教材知识体系整理，涵盖函数核心知识点及常见考点，建议结合具体例题进行深化理解。 - ```