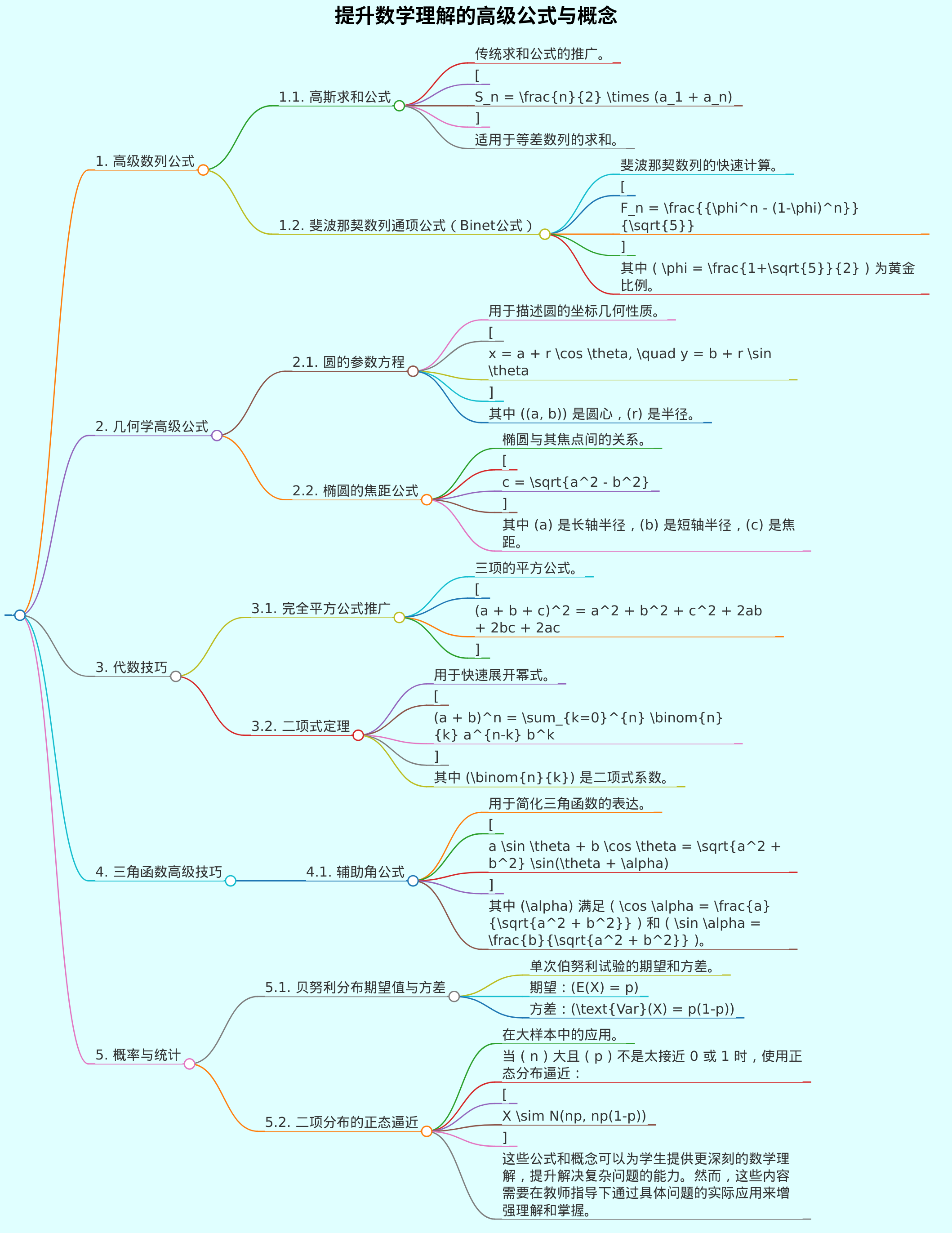
- 虽然中学数学的基础知识和公式在大多数国家和地区都是高度标准化的，但是随着数学研究的不断进展，新的方法和技巧可能会被开发出来以增加学习的深度和广度。以下是一些可能不在传统教材中出现，但对数学思维和理解有帮助的公式和概念： ## 1. 高级数列公式 ### 1.1. 高斯求和公式 - 传统求和公式的推广。 - \[ - S_n = \frac{n}{2} \times (a_1 + a_n) - \] - 适用于等差数列的求和。 ### 1.2. 斐波那契数列通项公式（Binet公式） - 斐波那契数列的快速计算。 - \[ - F_n = \frac{{\phi^n - (1-\phi)^n}}{\sqrt{5}} - \] - 其中 \( \phi = \frac{1+\sqrt{5}}{2} \) 为黄金比例。 ## 2. 几何学高级公式 ### 2.1. 圆的参数方程 - 用于描述圆的坐标几何性质。 - \[ - x = a + r \cos \theta, \quad y = b + r \sin \theta - \] - 其中 \((a, b)\) 是圆心，\(r\) 是半径。 ### 2.2. 椭圆的焦距公式 - 椭圆与其焦点间的关系。 - \[ - c = \sqrt{a^2 - b^2} - \] - 其中 \(a\) 是长轴半径，\(b\) 是短轴半径，\(c\) 是焦距。 ## 3. 代数技巧 ### 3.1. 完全平方公式推广 - 三项的平方公式。 - \[ - (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ac - \] ### 3.2. 二项式定理 - 用于快速展开幂式。 - \[ - (a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k - \] - 其中 \(\binom{n}{k}\) 是二项式系数。 ## 4. 三角函数高级技巧 ### 4.1. 辅助角公式 - 用于简化三角函数的表达。 - \[ - a \sin \theta + b \cos \theta = \sqrt{a^2 + b^2} \sin(\theta + \alpha) - \] - 其中 \(\alpha\) 满足 \( \cos \alpha = \frac{a}{\sqrt{a^2 + b^2}} \) 和 \( \sin \alpha = \frac{b}{\sqrt{a^2 + b^2}} \)。 ## 5. 概率与统计 ### 5.1. 贝努利分布期望值与方差 - 单次伯努利试验的期望和方差。 - 期望：\(E(X) = p\) - 方差：\(\text{Var}(X) = p(1-p)\) ### 5.2. 二项分布的正态逼近 - 在大样本中的应用。 - 当 \( n \) 大且 \( p \) 不是太接近 0 或 1 时，使用正态分布逼近： - \[ - X \sim N(np, np(1-p)) - \] - 这些公式和概念可以为学生提供更深刻的数学理解，提升解决复杂问题的能力。然而，这些内容需要在教师指导下通过具体问题的实际应用来增强理解和掌握。