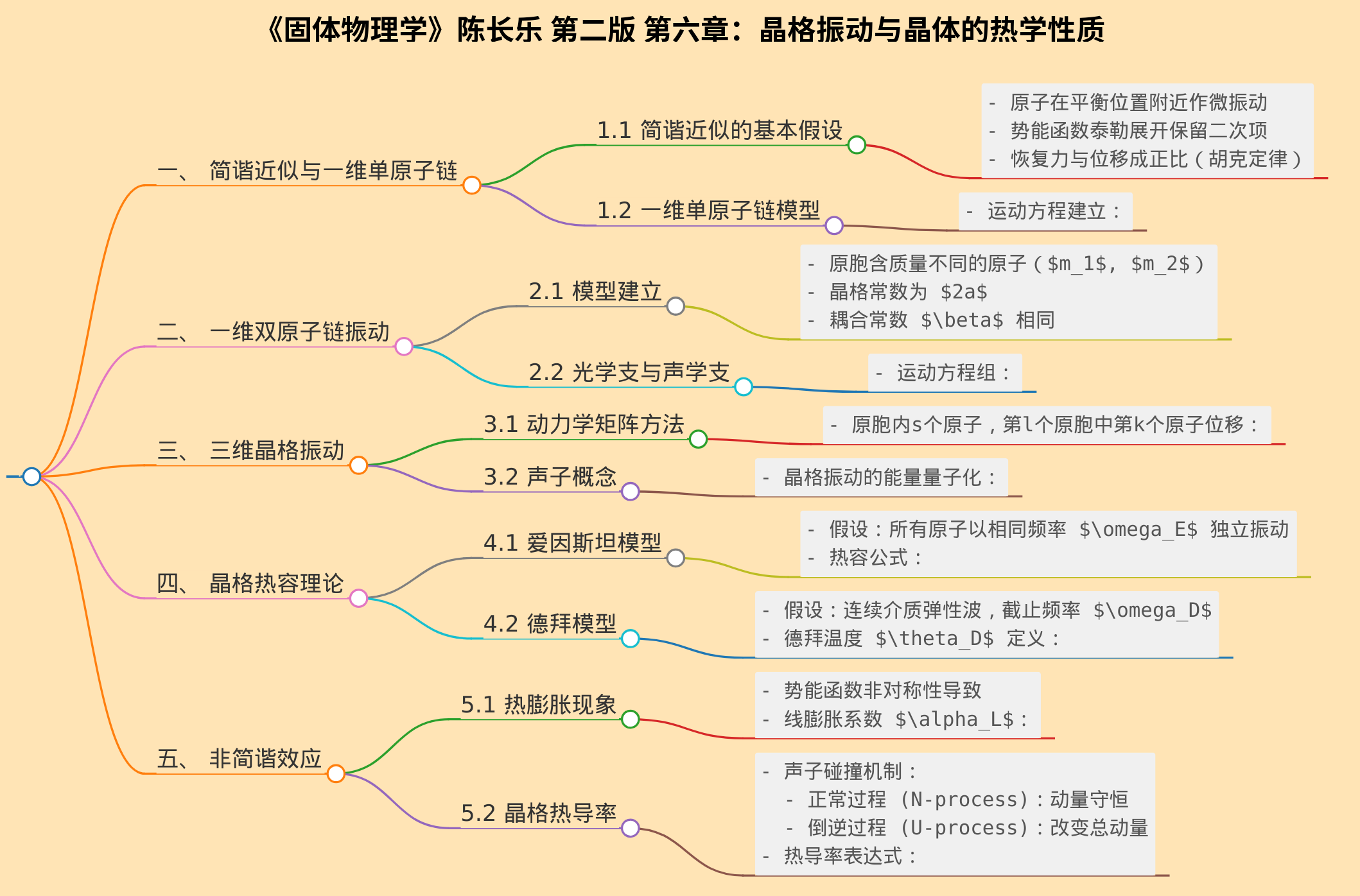
- ```markdown # 《固体物理学》陈长乐 第二版 第六章：晶格振动与晶体的热学性质 ## 一、 简谐近似与一维单原子链 ### 1.1 简谐近似的基本假设 - 原子在平衡位置附近作微振动 - 势能函数泰勒展开保留二次项 - 恢复力与位移成正比（胡克定律） ### 1.2 一维单原子链模型 - 运动方程建立： - $$ m \frac{d^2 u_n}{dt^2} = \beta (u_{n+1} + u_{n-1} - 2u_n) $$ - 格波解形式： - $$ u_n = A e^{i(qna - \omega t)} $$ - 色散关系推导： - $$ \omega(q) = 2\sqrt{\frac{\beta}{m}} \left| \sin\left(\frac{qa}{2}\right) \right| $$ - 第一布里渊区范围： $ q \in [-\pi/a, \pi/a] $ ## 二、 一维双原子链振动 ### 2.1 模型建立 - 原胞含质量不同的原子（$m_1$, $m_2$） - 晶格常数为 $2a$ - 耦合常数 $\beta$ 相同 ### 2.2 光学支与声学支 - 运动方程组： - $$ \begin{cases} - m_1 \ddot{u}_{2n} = \beta (v_{2n+1} + v_{2n-1} - 2u_{2n}) \\ - m_2 \ddot{v}_{2n+1} = \beta (u_{2n} + u_{2n+2} - 2v_{2n+1}) - \end{cases} $$ - 色散关系： - $$ \omega^2_{\pm} = \beta \left( \frac{1}{m_1} + \frac{1}{m_2} \right) \pm \beta \sqrt{\left( \frac{1}{m_1} + \frac{1}{m_2} \right)^2 - \frac{4}{m_1 m_2} \sin^2(qa)} $$ - 声学支特征： 同相振动，低频 - 光学支特征： 反相振动，高频 ## 三、 三维晶格振动 ### 3.1 动力学矩阵方法 - 原胞内s个原子，第l个原胞中第k个原子位移： - $$ \mathbf{u}_k(\mathbf{l}) = \frac{1}{\sqrt{m_k}} \sum_{\mathbf{q}} \mathbf{e}_k e^{i(\mathbf{q} \cdot \mathbf{R}_l - \omega t)} $$ - 动力学矩阵 $D(\mathbf{q})$ 定义： - $$ D_{kk'}^{\alpha\beta}(\mathbf{q}) = \frac{1}{\sqrt{m_k m_{k'}}} \sum_{\mathbf{l'}} \Phi^{\alpha\beta}_{kk'}(\mathbf{l},\mathbf{l'}) e^{i\mathbf{q} \cdot (\mathbf{R}_{l'} - \mathbf{R}_l)} $$ ### 3.2 声子概念 - 晶格振动的能量量子化： - $$ E_n = \left( n + \frac{1}{2} \right) \hbar \omega_j(\mathbf{q}) $$ - 声子性质： - 准粒子：能量 $\hbar \omega$，准动量 $\hbar \mathbf{q}$ - 玻色子：服从玻色-爱因斯坦统计 ## 四、 晶格热容理论 ### 4.1 爱因斯坦模型 - 假设：所有原子以相同频率 $\omega_E$ 独立振动 - 热容公式： - $$ C_V = 3N_A k_B \left( \frac{\theta_E}{T} \right)^2 \frac{e^{\theta_E/T}}{(e^{\theta_E/T} - 1)^2} $$ - （$\theta_E = \hbar \omega_E / k_B$） ### 4.2 德拜模型 - 假设：连续介质弹性波，截止频率 $\omega_D$ - 德拜温度 $\theta_D$ 定义： - $$ k_B \theta_D = \hbar \omega_D $$ - 热容表达式： - $$ C_V = 9Nk_B \left( \frac{T}{\theta_D} \right)^3 \int_0^{\theta_D/T} \frac{x^4 e^x}{(e^x - 1)^2} dx $$ - 低温极限 ($T \ll \theta_D$)： - $$ C_V \propto T^3 $$ ## 五、 非简谐效应 ### 5.1 热膨胀现象 - 势能函数非对称性导致 - 线膨胀系数 $\alpha_L$： - $$ \alpha_L = \frac{1}{L} \frac{dL}{dT} $$ ### 5.2 晶格热导率 - 声子碰撞机制： - 正常过程 (N-process)：动量守恒 - 倒逆过程 (U-process)：改变总动量 - 热导率表达式： - $$ \kappa = \frac{1}{3} C_v v \Lambda $$ - （$C_v$：热容，$v$：声速，$\Lambda$：平均自由程） - ``` - > 注：本拆解严格依据陈长乐《固体物理学》第二版第六章内容，重点涵盖： - > 1. 一维晶格振动理论（单/双原子链） - > 2. 三维晶格动力学与声子概念 - > 3. 晶格热容的量子理论（爱因斯坦/德拜模型） - > 4. 非简谐效应核心物理现象 - > 数学推导保留了关键公式，同时标注了核心物理概念的内在联系。