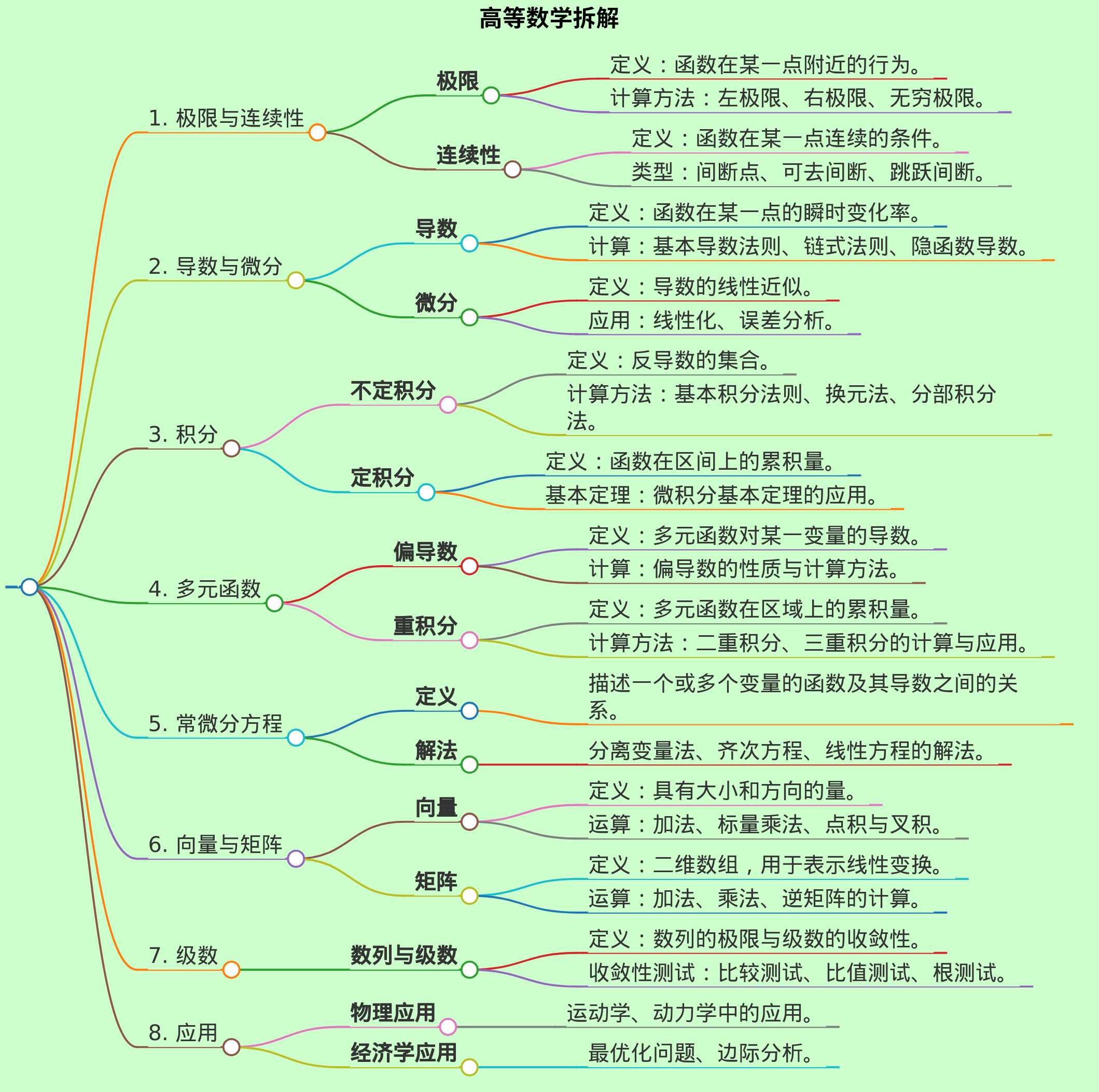
# 高等数学拆解 - 高等数学是数学的一个重要分支，通常包括以下几个主要内容。我们将其拆解为更小的模块，以便于理解和记忆。 ## 1. 极限与连续性 - **极限** - 定义：函数在某一点附近的行为。 - 计算方法：左极限、右极限、无穷极限。 - **连续性** - 定义：函数在某一点连续的条件。 - 类型：间断点、可去间断、跳跃间断。 ## 2. 导数与微分 - **导数** - 定义：函数在某一点的瞬时变化率。 - 计算：基本导数法则、链式法则、隐函数导数。 - **微分** - 定义：导数的线性近似。 - 应用：线性化、误差分析。 ## 3. 积分 - **不定积分** - 定义：反导数的集合。 - 计算方法：基本积分法则、换元法、分部积分法。 - **定积分** - 定义：函数在区间上的累积量。 - 基本定理：微积分基本定理的应用。 ## 4. 多元函数 - **偏导数** - 定义：多元函数对某一变量的导数。 - 计算：偏导数的性质与计算方法。 - **重积分** - 定义：多元函数在区域上的累积量。 - 计算方法：二重积分、三重积分的计算与应用。 ## 5. 常微分方程 - **定义** - 描述一个或多个变量的函数及其导数之间的关系。 - **解法** - 分离变量法、齐次方程、线性方程的解法。 ## 6. 向量与矩阵 - **向量** - 定义：具有大小和方向的量。 - 运算：加法、标量乘法、点积与叉积。 - **矩阵** - 定义：二维数组，用于表示线性变换。 - 运算：加法、乘法、逆矩阵的计算。 ## 7. 级数 - **数列与级数** - 定义：数列的极限与级数的收敛性。 - 收敛性测试：比较测试、比值测试、根测试。 ## 8. 应用 - **物理应用** - 运动学、动力学中的应用。 - **经济学应用** - 最优化问题、边际分析。 通过将高等数学拆解为这些模块，可以更容易地理解和掌握每个部分的内容。