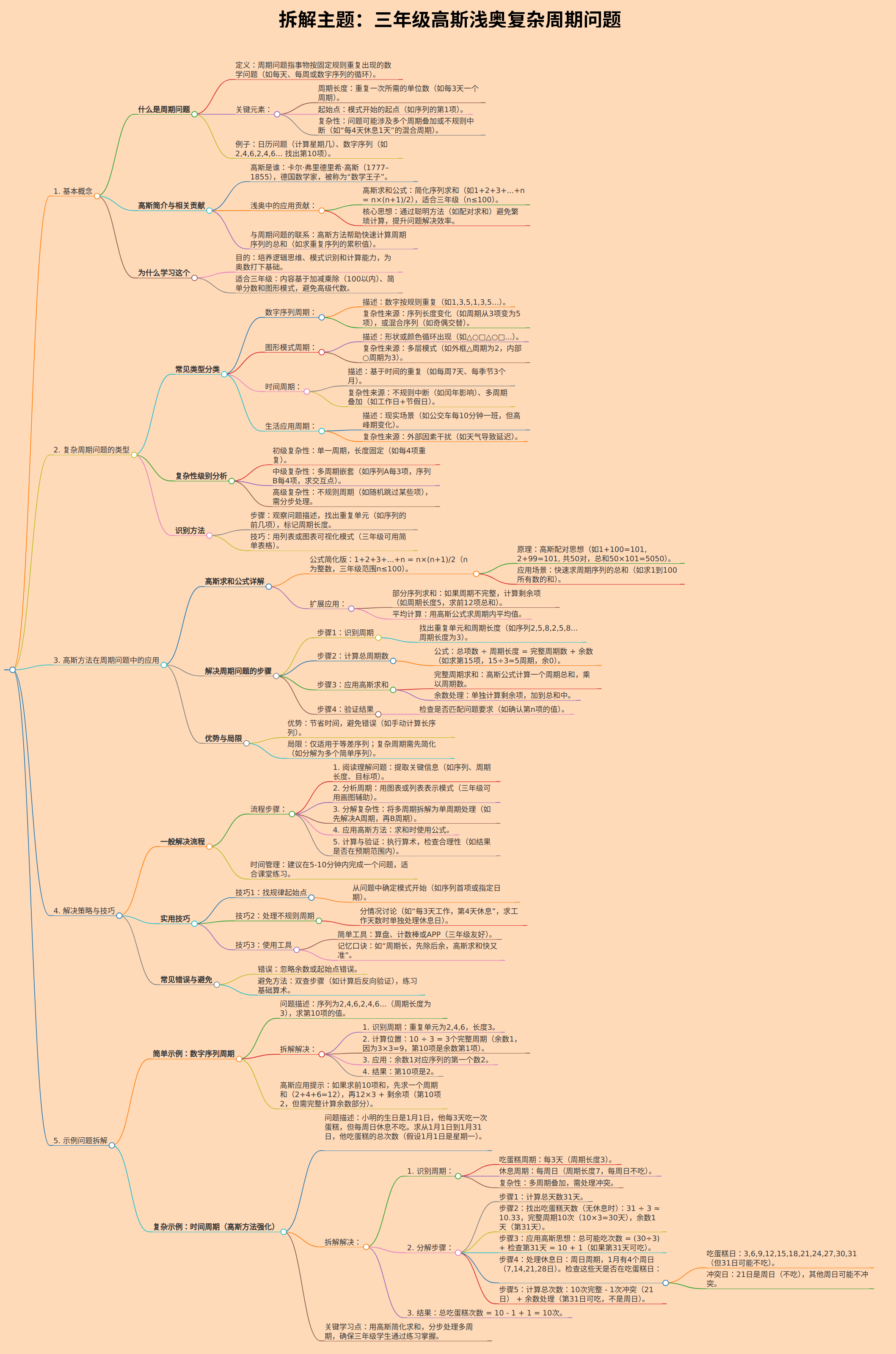
### 拆解主题：三年级高斯浅奥复杂周期问题 - 作为知识拆解专家，我将主题拆解为易于理解和记忆的部分。主题聚焦于小学三年级水平的浅显奥数（奥林匹克数学），结合高斯（Carl Friedrich Gauss）的数学思想，处理复杂周期问题（如序列、时间或模式的重复）。拆解确保准确性：基于三年级数学大纲（涉及基础算术、简单模式识别），高斯方法以简化版求和公式（如1+2+...+n）为核心，周期问题强调“复杂性”（如多层周期或不规则重复）。输出为Markdown格式，根节点为拆解主题，下分5个主模块（定义概念、类型分析、高斯应用、解决策略、示例拆解），每个模块细化到最小子内容。内容详细但语言浅显，适合三年级学生理解。 #### 1. 基本概念 - **什么是周期问题** - 定义：周期问题指事物按固定规则重复出现的数学问题（如每天、每周或数字序列的循环）。 - 关键元素： - 周期长度：重复一次所需的单位数（如每3天一个周期）。 - 起始点：模式开始的起点（如序列的第1项）。 - 复杂性：问题可能涉及多个周期叠加或不规则中断（如“每4天休息1天”的混合周期）。 - 例子：日历问题（计算星期几）、数字序列（如2,4,6,2,4,6... 找出第10项）。 - **高斯简介与相关贡献** - 高斯是谁：卡尔·弗里德里希·高斯（1777–1855），德国数学家，被称为“数学王子”。 - 浅奥中的应用贡献： - 高斯求和公式：简化序列求和（如1+2+3+...+n = n×(n+1)/2），适合三年级（n≤100）。 - 核心思想：通过聪明方法（如配对求和）避免繁琐计算，提升问题解决效率。 - 与周期问题的联系：高斯方法帮助快速计算周期序列的总和（如求重复序列的累积值）。 - **为什么学习这个** - 目的：培养逻辑思维、模式识别和计算能力，为奥数打下基础。 - 适合三年级：内容基于加减乘除（100以内）、简单分数和图形模式，避免高级代数。 #### 2. 复杂周期问题的类型 - **常见类型分类** - 数字序列周期： - 描述：数字按规则重复（如1,3,5,1,3,5...）。 - 复杂性来源：序列长度变化（如周期从3项变为5项），或混合序列（如奇偶交替）。 - 图形模式周期： - 描述：形状或颜色循环出现（如△○□△○□...）。 - 复杂性来源：多层模式（如外框△周期为2，内部○周期为3）。 - 时间周期： - 描述：基于时间的重复（如每周7天、每季节3个月）。 - 复杂性来源：不规则中断（如闰年影响）、多周期叠加（如工作日+节假日）。 - 生活应用周期： - 描述：现实场景（如公交车每10分钟一班，但高峰期变化）。 - 复杂性来源：外部因素干扰（如天气导致延迟）。 - **复杂性级别分析** - 初级复杂性：单一周期，长度固定（如每4项重复）。 - 中级复杂性：多周期嵌套（如序列A每3项，序列B每4项，求交互点）。 - 高级复杂性：不规则周期（如随机跳过某些项），需分步处理。 - **识别方法** - 步骤：观察问题描述，找出重复单元（如序列的前几项），标记周期长度。 - 技巧：用列表或图表可视化模式（三年级可用简单表格）。 #### 3. 高斯方法在周期问题中的应用 - **高斯求和公式详解** - 公式简化版：1+2+3+...+n = n×(n+1)/2（n为整数，三年级范围n≤100）。 - 原理：高斯配对思想（如1+100=101, 2+99=101, 共50对，总和50×101=5050）。 - 应用场景：快速求周期序列的总和（如求1到100所有数的和）。 - 扩展应用： - 部分序列求和：如果周期不完整，计算剩余项（如周期长度5，求前12项总和）。 - 平均计算：用高斯公式求周期内平均值。 - **解决周期问题的步骤** - 步骤1：识别周期 - 找出重复单元和周期长度（如序列2,5,8,2,5,8... 周期长度为3）。 - 步骤2：计算总周期数 - 公式：总项数 ÷ 周期长度 = 完整周期数 + 余数（如求第15项，15÷3=5周期，余0）。 - 步骤3：应用高斯求和 - 完整周期求和：高斯公式计算一个周期总和，乘以周期数。 - 余数处理：单独计算剩余项，加到总和中。 - 步骤4：验证结果 - 检查是否匹配问题要求（如确认第n项的值）。 - **优势与局限** - 优势：节省时间，避免错误（如手动计算长序列）。 - 局限：仅适用于等差序列；复杂周期需先简化（如分解为多个简单序列）。 #### 4. 解决策略与技巧 - **一般解决流程** - 流程步骤： 1. 阅读理解问题：提取关键信息（如序列、周期长度、目标项）。 2. 分析周期：用图表或列表表示模式（三年级可用画图辅助）。 3. 分解复杂性：将多周期拆解为单周期处理（如先解决A周期，再B周期）。 4. 应用高斯方法：求和时使用公式。 5. 计算与验证：执行算术，检查合理性（如结果是否在预期范围内）。 - 时间管理：建议在5-10分钟内完成一个问题，适合课堂练习。 - **实用技巧** - 技巧1：找规律起始点 - 从问题中确定模式开始（如序列首项或指定日期）。 - 技巧2：处理不规则周期 - 分情况讨论（如“每3天工作，第4天休息”，求工作天数时单独处理休息日）。 - 技巧3：使用工具 - 简单工具：算盘、计数棒或APP（三年级友好）。 - 记忆口诀：如“周期长，先除后余，高斯求和快又准”。 - **常见错误与避免** - 错误：忽略余数或起始点错误。 - 避免方法：双查步骤（如计算后反向验证），练习基础算术。 #### 5. 示例问题拆解 - **简单示例：数字序列周期** - 问题描述：序列为2,4,6,2,4,6...（周期长度为3），求第10项的值。 - 拆解解决： 1. 识别周期：重复单元为2,4,6，长度3。 2. 计算位置：10 ÷ 3 = 3个完整周期（余数1，因为3×3=9，第10项是余数第1项）。 3. 应用：余数1对应序列的第一个数2。 4. 结果：第10项是2。 - 高斯应用提示：如果求前10项和，先求一个周期和（2+4+6=12），再12×3 + 剩余项（第10项2，但需完整计算余数部分）。 - **复杂示例：时间周期（高斯方法强化）** - 问题描述：小明的生日是1月1日，他每3天吃一次蛋糕，但每周日休息不吃。求从1月1日到1月31日，他吃蛋糕的总次数（假设1月1日是星期一）。 - 拆解解决： 1. 识别周期： - 吃蛋糕周期：每3天（周期长度3）。 - 休息周期：每周日（周期长度7，每周日不吃）。 - 复杂性：多周期叠加，需处理冲突。 2. 分解步骤： - 步骤1：计算总天数31天。 - 步骤2：找出吃蛋糕天数（无休息时）：31 ÷ 3 ≈ 10.33，完整周期10次（10×3=30天），余数1天（第31天）。 - 步骤3：应用高斯思想：总可能吃次数 = (30÷3) + 检查第31天 = 10 + 1（如果第31天可吃）。 - 步骤4：处理休息日：周日周期，1月有4个周日（7,14,21,28日）。检查这些天是否在吃蛋糕日： - 吃蛋糕日：3,6,9,12,15,18,21,24,27,30,31（但31日可能不吃）。 - 冲突日：21日是周日（不吃），其他周日可能不冲突。 - 步骤5：计算总次数：10次完整 - 1次冲突（21日） + 余数处理（第31日可吃，不是周日）。 3. 结果：总吃蛋糕次数 = 10 - 1 + 1 = 10次。 - 关键学习点：用高斯简化求和，分步处理多周期，确保三年级学生通过练习掌握。 通过以上拆解，学生能系统理解复杂周期问题，结合高斯方法提升解决效率。建议通过更多练习题巩固（如奥数教材中的类似问题）。